1
MONETARY POLICY NEAR THE ZERO LOWER BOUND
(2015) finds that there is a 14 per cent probability of the cash rate being at zero by
February 2017.
(2015) finds a 14 per cent probability that the cash rate will reach zero by February 2017.
D15/127109
GENERAL
1

Economist
Research
Economic Research Department
21 April 2015
D15/127109
GENERAL
2

Resources
M (2015), ‘Estimates of Uncertainty around the Market-implied Cash Rate Path’, ER internal
note.
D15/127109
GENERAL
3

2
THE PROBABILITY OF REACHING THE ZERO LOWER BOUND
If forward rates make the same size errors as they have in the past, there is a 41 per cent probability of a zero
cash  rate  at  December  quarter  2021.  Stochastic  simulations  of  MARTIN  imply  a  similar  probability  of
37 per cent.
The August SMP assumed the cash rate will decline to 42 basis points by mid‐2021. This raises the prospect
that  monetary  policy  could  soon  be  constrained  by  the  zero  lower  bound  (ZLB),  limiting  the  ability  of
monetary policy to offset future negative shocks.
(2015) calculates the distribution of historic errors in market expectations of the cash rate at different
horizons (Graph 1). Assuming the market makes similarly sized errors to those in the past gives the probability
that the cash rate will be constrained at the ZLB. Updated estimates using this approach are shown as the
orange line in Graph 2. The probability of reaching the ZLB is estimated to be 34 per cent at December 2020,
and 41 per cent at December 2021. The blue line in Graph 2 shows the probability of reaching the ZLB using
stochastic simulations in MARTIN (
forthcoming). 1
Graph 1
Graph 2
Cash Rate and Market-implied Path
Probability of Zero Cash Rate at Horizon*
Quarterly
As at August 2019 SMP
%
%
%
%
10
10
Forward rate errors
40
40
8
8
30
30
MARTIN
6
6
(preliminary)
Zero-coupon
forward rate
20
20
4
4
Cash rate target
10
10
2
2
Aug SMP projection
0
0
0
0
1996
2001
2006
2011
2016
2021
M
J
S
D
M
J
S
D
M
J
S
D
Source: RBA
2019
2020
2021
Source: RBA
The  two  approaches  have  different  strengths  and  weaknesses. MARTIN’s  estimates  depend  on  many
assumptions and estimates. In particular, they assume that the cash rate follows a calibrated Taylor‐type rule
(see
&
2018) which is a very simple approximation to past RBA behaviour. The yield curve
approach assumes that the OIS curve makes the same size errors as it has in the past. In contrast to MARTIN,
forward rates should encompass all available information. Accordingly, unless one thought that forward rates
are  seriously  biased  or  misinformed,  yield  curve  errors  provides  more  credible  point  estimates  of  the
probability than MARTIN’s stochastic simulations. However, the two big advantages of using MARTIN are that
it enables estimation of how alternative policies might interact with the ZLB, and can quantify the costs of
constrained monetary policy (for example, in terms of additional unemployment). Both issues are discussed
in more detail in
(forthcoming). That said, the most important point is that both methods produce
very similar results, despite being constructed independently.
These results have important policy implications – if the probability of a zero cash rate is high, monetary
policy should arguably be more expansionary than would otherwise be the case, as discussed in
2015,
2016 and
2015).
Research Economist
Economic Research Department
21 August 2019
1   Thanks to
for helpful comments and running the MARTIN simulations.
D19/374060
GENERAL
1

Appendix A ‐ Measurement details
Following
(2015), I use zero‐coupon forward rates as a measure of market expectations for the path of
the  cash rate. These forward rates are constructed  using overnight index swap (OIS) rates, and yields on
Treasury  notes  and  Commonwealth  Government  Securities.  To  calculate  historic  errors  in  cash  rate
expectations, I take the market‐implied path of the cash rate on the first Wednesday of the months in which
the  SMP  is  released.  This  should  approximately  reflect  the  cash  rate  expectations  on  which  the  Bank’s
forecasts have been conditioned. The cash rate `forecast error’ is then defined as the realised cash rate target
minus the corresponding zero‐coupon forward rate. I use EA’s cash rate assumption from the August SMP as
the baseline cash rate path.
In calculating the probabilities presented in this note I have used historic absolute forward‐rate errors. Doing
so assumes that the forward curve is an unbiased forecast of the cash rate. An alternative approach could be
to assume that the  cash rate forecast  errors follow the same distribution as  the historical distribution  of
actual forecast errors. Under this approach, the probability of zero cash rate at December quarter 2021 is
60 per cent.
D19/374060
GENERAL
2

link to page 6

3
THE EFFECTIVE LOWER BOUND AND ITS IMPLICATIONS
As  the  cash  rate  declines,  the  possibility  of  reaching  its  Effective  Lower  Bound  (ELB)  becomes  a  more
pressing concern. Stochastic simulations in MARTIN show that the likelihood of a zero cash rate in December
2021 has risen to around 40 per cent as at the August 2019 SMP from around 20 per cent at the May 2019
SMP.
Introduction
In this note I estimate the probability of reaching the ELB using MARTIN, incorporate an ELB in to MARTIN’s
policy rule and discuss some of the implications of being constrained by the lower bound.
Probability of reaching the ELB
Stochastic simulations in MARTIN estimate that the likelihood of reaching an ELB is relatively high and has
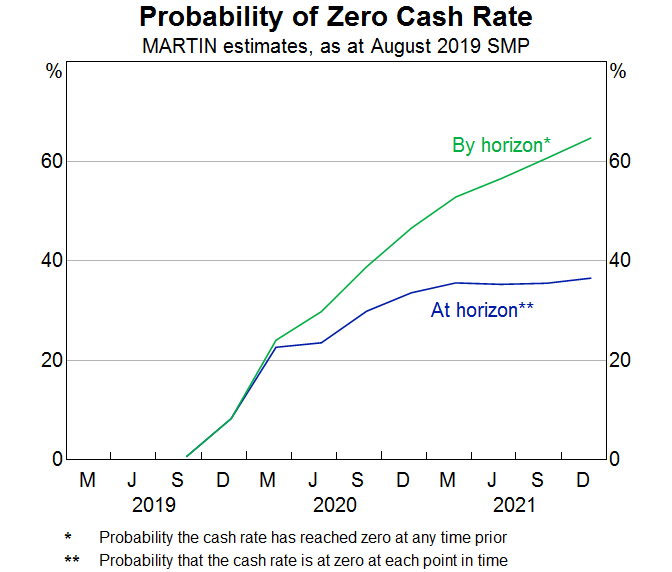
increased recently (Graph 1).3 For example, there is a 37 per cent chance of being at the zero lower bound
at the end of the forecast horizon, according to MARTIN. This estimate was just 18 per cent at the May 19
SMP.  Non-parametric methods using market  pricing produce similar results  (
2019).  If we measure
the probability of having reached a cash rate of zero by the forecast horizon, instead of necessarily being at
zero at the forecast horizon, the estimate is around 60 per cent.
Graph 1
.
3   I use 10,000 draws of historical errors, apply these errors as shocks to MARTIN and measure how many of the scenarios result
in a cash rate at or below 0. See
2019 for more detail on stochastic simulations in MARTIN.
D19/196145
GENERAL
1

Limitations and further work
This work abstracts from agents’ expectations of future monetary policy, which are likely to be an
important element when the central bank is constrained by the ELB. Further work will look to incorporate
expectations into the ELB framework presented in this note.
Conclusion
Stochastic simulations in MARTIN show that the likelihood of a zero cash rate in December 2021 has risen
in recent months to around 40 per cent as at the August 2019 SMP. Simple
Macroeconomic Modelling
Economic Analysis Department
8 October 2019
D19/196145
GENERAL
6

link to page 8 4
ESTIMATES OF UNCERTAINTY AROUND THE MARKET-IMPLIED CASH RATE PATH
This  note  estimates  the  uncertainty  around  a  market-implied  path  of  the  cash  rate  using  the  historical
distribution of differences between zero-coupon forward rates and the actual cash rate target. The width of
the estimated 90 per cent confidence interval is about ±3 percentage points at the two-year horizon. If the
distribution of forward-rate errors is similar to that over the past two decades, the market path at the time
of the February SMP implies that the probability of a zero cash rate in February 2017 is 14 per cent.
Introduction
Forecasts  presented  in  the  February  Statement  on  Monetary  Policy  (SMP)  were  conditioned  on  the
assumption that the cash rate moves broadly in line with expectations inferred from market pricing.1 While
the SMP was careful to stress that ‘this assumption does not represent a commitment by the Board to any
particular path for policy’, it may be desirable to reinforce this point. One way of doing this is by graphically
presenting confidence intervals around the market-implied cash rate path (i.e. the cash rate ‘forecast’), as
is  done  for  the  SMP  forecasts  of  GDP  growth,  inflation  and,  more  recently,  unemployment.  Additionally,
estimates of uncertainty around the cash rate forecast can be used to estimate the probability of the cash
rate  reaching  zero, which may  be  an  important  consideration  when  determining  the  appropriate  path of
policy.2
Some  other  central  banks  present  measures  of  uncertainty  around  their  policy  rate  projections.  For
example,  the  US  Federal  Reserve  publishes  model-based  confidence  intervals  and  the  distribution  of
Federal Open Market Committee participants’ projections of the appropriate path of the federal funds rate.
The Riksbank  publishes a forecast repo rate path, with confidence intervals based on the Riksbank’s own
forecasting errors and the historical ability of forward rates to forecast the repo rate (Kjellberg and Villani
2010;  Sveriges  Riksbank  2015).3 Norges  Bank  publishes  forecasts  of  the  ‘key  policy  rate’  based  on
judgement  about  the  appropriate  path  of  monetary  policy,  with  confidence  intervals  generated  using  a
macroeconomic model (Norges Bank 2005, 2014).
Graph 1
Cash Rate and Market-implied Path
Data and methodology
Quarterly
%
%
I  use  estimated  zero-coupon  forward  rates  as  a
measure of market expectations for the path of the
10
10
cash  rate  (Graph 1).  These  forward  rates  are
Zero-coupon
forward rate
constructed using overnight index swap (OIS) rates,
8
8
and  yields  on  Treasury  notes  and  Commonwealth
Government  Securities.4 For  the  purposes  of  this
6
6
analysis,  the  market-implied  path  of  the  cash  rate
4
4
is taken as being the zero-coupon forward curve on
Cash rate target
the  first  Wednesday  of  the  months  in  which  the
2
2
SMP is released (i.e. the day after the Board’s cash
rate  decision),  as  this  should  be  a  reasonable
0
0
approximation  of  the  cash  rate  expectations  on
1993
1999
2005
2011
2017
which  the  Bank’s  SMP  forecasts  could  be
Source: RBA
conditioned. The realised cash rate target is taken to be the cash rate target on the same days. The cash
rate  ‘forecast  error’  is  defined  as  the  realised  cash  rate  target  minus  the  corresponding  zero-coupon
1   In previous SMPs, forecasts were conditioned on the assumption of a constant cash rate.
2
(forthcoming) reviews  the literature discussing  the appropriate  setting of monetary  policy given the existence of a
lower bound on nominal interest rates.
3     The  Riksbank  uses  two  sources  of  forecasts  errors  because  the  history  of  its  own  forecasts  is  too  short  to  precisely  estimate
confidence intervals around the repo rate projection.
4   There  are  three  main  sources  of  data  used  by  the  Bank  to  infer  market-implied  cash  rate  expectations:  interbank  cash  rate
futures (e.g. Figure 4.1 of the February SMP); OIS (e.g. DM Monthly Note – March 2015); and estimated zero-coupon forward
rates (e.g. Statistical Table F17, Finlay and Chambers (2008) and Finlay and Olivan (2012) – see these papers for details on how
the  zero-coupon  forward  rates  are  estimated).  Differences  between  cash  rate  expectations  implied  by  these  data  sources
appear to be small. I use zero-coupon forward rates because of their longer horizon and availability from an earlier date.
D15/126403
1

link to page 9 link to page 9 forward rate. Cash rate forecast errors are calculated at quarterly horizons up to nine quarters ahead over
the inflation-targeting period.
Summary statistics
Table 1 presents statistics describing cash rate forecast errors. The market-implied cash rate path appears
to  be  roughly  unbiased  at  short  horizons,  but  the  size  of  the  average  error  (or  bias)  increases  with  the
horizon  (although  it  is not significantly  different to zero at the 5 per cent level of significance  at  forecast
horizons  less  than  eight  quarters  ahead).  The  bias  at  longer  horizons  could  reflect  the  existence  of  a
positive  term  premium  (discussed  below).  The  average  magnitude  of  errors,  as  measured  by  the  mean
absolute error (MAE) and root-mean-square error (RMSE), also increases with the forecast horizon.
Table 1: Cash Rate Forecast Errors Based on Zero-coupon Forward Rates – Summary Statistics
Percentage points
Forecast horizon
One quarter
Two quarters
Four quarters
Eight quarters
0.04
−0.06
−0.21
−0.67
Average error(a)
(0.22)
(0.48)
(0.26)
(0.03)
MAE
0.23
0.39
0.81
1.39
RMSE
0.34
0.64
1.07
1.56
Maximum absolute error
1.59
3.36
3.64
3.84
Forecast origin
August 2008
August 2008
May 2008
February 1995
No. of observations
86
85
83
79
(a) p-values (in brackets) based on a constant-only regression with Newey-West standard errors
Source: RBA
Confidence intervals
Graph 2 presents the 70th and 90th percentiles of the historical distribution of absolute forecast errors.5 As
expected, the percentiles tend to increase with the forecast horizon; the 90th percentile of absolute four-
quarter-ahead forecast errors is around 1.7 percentage points, while it is around 2.9 percentage points at
the eight-quarter-ahead horizon. Using the distribution of absolute forecast errors to construct confidence
intervals  assumes  that  the  distribution  of  forecast  errors  is  symmetric  and  centred  at  zero;  that  is,  it
assumes that any bias and skewness in the sample of forward-rate errors will not persist into the future (it
is  not  necessary  to  assume  normality).  These  are  the  same  assumptions  made  in  constructing  the
confidence intervals presented in the SMP.
Graph 2
Graph 3
Cash Rate Forecast Confidence Intervals*
Cash Rate Forecast*
Percentiles of absolute forecast errors since 1993
Quarterly
ppt
ppt
%
%
90th percentile
70 per cent
interval
2
2
4
4
70th percentile
1
1
2
2
0
0
90 per cent interval
1
2
3
4
5
6
7
8
9
0
0
Horizon: quarters from forecast origin
2012
2013
2014
2015
2016
2017
* Forecasts based on zero-coupon forward rates
* Based on zero-coupon forward rates
Source: RBA
Source: RBA
5   This choice of percentiles matches those used in constructing the confidence intervals presented in the SMP.
D15/126403
2

link to page 9 link to page 10 Graph 3  shows  the  market-implied  cash  rate  path  as  at  the  February  2015  SMP,  along  with  the
70 and 90 per cent confidence intervals based on the distribution of absolute forecast errors. The intervals
are substantially wider than some alternatives. For example, the 90 per cent probability interval around the
Economic  Research  (ER)  model-based  cash  rate  forecast  is  around  ±2 percentage  points  at  the  two-year
horizon,  although  this  partly  reflects  the  fact  that  this  interval  is  based  on  in-sample  fit,  rather  than  on
historical  out-of-sample  forecasting  performance.6 The  market-implied  intervals  are  also  probably  wider
than  some  people’s  subjective  assessment  of  current  uncertainty  around  the  path  of  the  cash  rate.
However, psychological studies find that subjective estimates of uncertainty tend to be too low (often by
large margins), even among experts.7
In  presenting  the  confidence  intervals,  I  truncate  them  at  zero,  consistent  with  the  approach  taken  by
Norges Bank (Norges Bank 2014).8 However, in reality the effective lower bound on the nominal policy rate
may  be  different  to  zero  for  technical  reasons.  For  example,  the  Fed  and  Bank  of  England  have  positive
effective  lower  bounds,  while  the  Riksbank  and  the  Swiss  National  Bank  currently  have  negative  policy
rates.  In  contrast  to  the  approach  taken  here,  the  Riksbank  does  not  truncate  its  repo  rate  forecast
distribution at a lower bound, so that the  forecast distribution has considerable probability mass at repo
rates as low as −2 per cent (Sveriges Riksbank 2015). This may strike some readers as implausible. However,
Kjellberg  and  Villani  (2010)  argue  that  this  can  be  justified  in  two  ways:  1)  the  zero  lower  bound  is  not
exactly zero, implying that moderately negative interest rates cannot be ruled out; and 2) negative policy
rates in the forecast distribution can be taken to represent alternative monetary policy measures with the
same effect as though the policy rate were negative.
Probability of reaching the zero lower bound
Graph 4
Probability of Zero Cash Rate at Horizon*
The  intersection  of  the  horizontal  axis  and  the
As at February 2015 SMP
confidence  intervals  in  Graph  3  provides  an
%
%
estimate of the probability of a zero cash rate at a
Based on historical distribution
of forecast errors
given  forecast  horizon,  conditional  on  the  market-
30
30
implied cash rate path at the time of the February
SMP.  The  pink  line  in  Graph 4  shows  this
20
20
probability at different forecast horizons, assuming
that  the  distribution  of  absolute  forward-rate
errors  is  the  same  as  over  the  past  two  decades
10
10
and that these errors are symmetrically distributed
Based on historical
distribution of absolute
around  zero.  The  market  path  implies  that  the
forecast errors
0
0
probability of the cash rate being at the zero lower
May-15
Nov-15
May-16
Nov-16
May-17
bound  is  5 per  cent  in  February  2016  and  14  per
Horizon
cent in February 2017.
* Based on zero-coupon forward rates
Source: RBA
Using absolute errors assumes  that the  forward  curve  provides an unbiased forecast of the cash rate. As
mentioned above, this assumption is also made in constructing the SMP confidence intervals, although the
rationale differs here. Tulip and Wallace (2012) argue that any bias in economic forecasts should not persist
into the future, since it is in the forecaster’s interest to generate unbiased forecasts. However, in the case
of  the  cash  rate,  this  assumption  is  equivalent  to  assuming  that  any  term  premia  in  the  zero-coupon
forward rates are zero on average. However, this might not be the case if investors require (or a willing to
pay) a premium for holding longer-maturity assets.
An  alternative  approach  is  to  assume  that  cash  rate  forecast  errors  follow  the  same  distribution  as  the
historical distribution of actual forecast errors. This allows the forecast error distribution to have  a mean
equal  to  the  average  forward-rate  error,  which  can  be  interpreted  as  the  average  term  premium.  It  also
preserves the historical skewness in the data. Under this approach, shown as the purple line in Graph 4, the
6   See Graph 3 in
and
(2015) (restricted).
7   See Kahneman, Slovic and Tversky (1982) (Part VI, titled ‘Overconfidence’) or, for an accessible summary, the Wikipedia (2012)
entry ‘Overconfidence Effect’.
8   Truncation means that forward rates represent the median but not the mean of the  cash rate forecast distribution, since the
truncated  distribution  is  asymmetric.  However,  the  expectations  theory  of  the  yield  curve  implies  that  forward  rates  should
equal the mean. I ignore this complication here, but recognise that it would need to be addressed in further work.
D15/126403
3

link to page 11 probability  of  a  zero  cash  rate  is  estimated  to  be  9 per  cent  in  February  2016  and  27  per  cent  in
February 2017. These probabilities are substantially higher than those based on the historical distribution
of absolute forecast errors, because the sample includes more large negative forecast errors (i.e. where the
realised  cash  rate  turned  out  to  be  substantially  lower  than  forecast)  than  large  positive  forecast  errors
(Graph 5).
Graph 5
Although  the  purple  line  in  Graph  4  is  simpler  to
Histogram of Cash Rate Forecast Errors*
construct  and  explain,  and  requires  fewer
Relative frequency, eight-quarter-ahead horizon
assumptions, the pink line will be more valid if the
%
%
apparent bias in the market-implied path at longer
horizons  has  arisen  by  chance  and  is  likely  to
20
20
disappear.  Consistent  with  this,  Finlay  and
Chambers  (2008)  find  evidence  to  suggest  that
15
15
term  premia  at  maturities  up  to  five  years  were
small  and  negative  through  most  of  the  inflation-
10
10
targeting  period  up  to  2007  (although  they  were
positive  and  relatively  large  in  the  mid  1990s,
5
5
which  coincides  with  several  large  negative  cash
rate  forecast  errors).  Additionally,  the  cash  rate
0
0
expectations  presented  in  the  DM  Monthly  Note
<-3
-3 to -2 -2 to -1 -1 to 0
0 to 1
1 to 2
2 to 3
>3
and the SMP are not adjusted for term premia.9
* Based on zero-coupon forward rates
Source: RBA
Stability of uncertainty measures
The estimates in this note are conditional on the shocks experienced during the inflation-targeting period,
but this may not be representative of the shocks that will be experienced in the future. Specifically, there
may be periods when the path of the cash rate is more or less uncertain (i.e. the cash rate forecast errors
could  be  heteroskedastic).  This  might  be  the  case  if,  for  instance,  the  Bank’s  communications  and  policy
reaction function have become clearer, so that market participants are better able to predict the path of
the cash rate, or if the variance of economic shocks has declined.
As a rough test of the stability of the variance of the forecast error distribution, I regress the squared cash
rate forecast errors on a constant and a dummy variable that is equal to one after the Bank began explicitly
publishing  its  forecasts  in  the  SMP  (February  2007).  I  use  Newey-West  standard  errors  to  account  for
autocorrelation.  I  am  unable  to  reject  the  null  hypothesis  that  the  coefficient  of  the  dummy  variable  is
equal  to  zero  at  any  of  the  forecast  horizons  considered,  suggesting  that  improvements  in  the  Bank’s
communication have not improved the market’s ability to forecast changes in the cash rate. However, this
test is fairly rudimentary and the results are sensitive to the exclusion of the large forecast errors arising
during  the  global  financial  crisis.  At  face  value,  the  results  provide  little  evidence  to  suggest  that  the
variance of the forecast error distribution, and thus the width of the confidence intervals, has changed over
time.
Conclusion
As the discussion above indicates, different assumptions about bias, skewness, stability and so on could be
made  in  estimating  uncertainty  about  the  market-implied  cash  rate  path.  Although  these  would  change
numerical  estimates,  they  are  unlikely  to  greatly  change  the  qualitative  results.  Specifically,  uncertainty
about the future cash rate is large (arguably, this is the  key point that publication of confidence intervals
needs to convey) and the probability of hitting the zero lower bound is substantial.
Economist
Economic Research Department
14 April 2015
9   Some central banks adjust forward rates for the existence of risk premia. For example, the Fed uses a rule-of-thumb that the
term  premium  is  equal  to  one  basis  point  per  month  (e.g.  Board  of  Governors  of  the  Federal  Reserve  System  2009).  Up  to
September 2008, the Riksbank adjusted forward rates at each horizon by subtracting the average forward-rate error (Kjellberg
and Villani 2010). Since then, the Riksbank has adjusted forward rates by subtracting model-based estimates of risk premia.
D15/126403
4

References
Board of Governors of the Federal Reserve System (2009), Monetary Policy Alternatives, December.
Finlay  R  and  M  Chambers  (2008),  ‘A  Term  Structure  Decomposition  of  the  Australian  Yield  Curve’,  RBA
Research Discussion Paper No 2008-09.
Finlay  R  and  D  Olivan  (2012),  ‘Extracting  Information  from  Financial  Market  Instruments’,  RBA  Bulletin,
March, pp 45–54.
Kahneman  D,  P  Slovic  and  A  Tversky  (eds)  (1982),  Judgment  under  Uncertainty:  Heuristics  and  Biases,
Cambridge University Press, Cambridge.
Kjellberg D and M Villani (2010), ‘The Riksbank’s Communication of Macroeconomic Uncertainty’, Sveriges
Riksbank Economic Review, 1, pp 5–41.
D (forthcoming), ‘Monetary Policy near the Zero Lower Bound’, internal ER note.
Norges  Bank  (2005),  ‘Uncertainty  Surrounding  Future  Interest  Rate  Developments’,  Inflation  Report,
3/2005, pp 19–21.
Norges Bank (2014), Monetary Policy Report, 4/2014.
Sveriges Riksbank (2015), Monetary Policy Report, February.
Tulip  P  and  S  Wallace  (2012),  ‘Estimates  of  Uncertainty  around  the  RBA's  Forecasts’,  RBA  Research
Discussion Paper No 2012-07.
Wikipedia (2012), ‘Overconfidence Effect’, accessed 10 January 2012.
D15/126403
5

5
ALTERNATIVE INTEREST RATE PATHS – APRIL 2015
Forecast targeting1
D15/145971
1

Given  the  market-implied  cash  rate  path  in  the  baseline  scenario,  and  assuming  that
uncertainty around this cash rate forecast is as estimated in
(2015), the probability of a zero cash rate
in two years’ time is 15 per cent (Graph 2).2
Graph 2
Probability of Zero Cash Rate at Horizon*
As at April 2015
%
%
15
15
10
10
5
5
0
0
Jul-15
Jan-16
Jul-16
Jan-17
Horizon
* Based on market-implied cash rate path and the historical ability of zero-
coupon forward rates to forecast the cash rate; assumes forecast errors
are symmetric
Source: RBA
and
/Economists/Economic Research Department/23 April 2015
2   This  estimate  assumes  that  cash  rate  forecast  errors  follow  the  same  distribution  as  the  historical  distribution  of  absolute
forecast errors (based on zero-coupon forward rates) and that these errors are symmetrically distributed around the cash rate
forecast;  assuming  that  cash  rate  forecast  errors  follow  the  historical  distribution  of  actual  errors  results  in  a  substantially
higher probability of the cash rate reaching zero.
D15/145971
2

6
ALTERNATIVE INTEREST RATE PATHS – JULY 2015
Forecast targeting
D15/259070
1

link to page 16 Given the market-implied cash rate path in the baseline scenario, and assuming that
uncertainty around this cash rate forecast is as estimated in
(2015), the probability of a zero cash rate
in two years’ time is 15 per cent (Graph 2).2
Graph 2
Probability of Zero Cash Rate at Horizon*
As at July 2015
%
%
15
15
10
10
5
5
0
0
Oct-15
Apr-16
Oct-16
Apr-17
Horizon
* Based on market-implied cash rate path and the historical ability of zero-
coupon forward rates to forecast the cash rate; assumes forecast errors
are symmetric
Source: RBA
Economist/Economic Research Department/20 July 2015
2 This estimate assumes that cash rate forecast errors fol ow the same distribution as the historical distribution of absolute
forecast errors (based on zero-coupon forward rates) and that these errors are symmetrically distributed around the cash rate
forecast; assuming that cash rate forecast errors follow the historical distribution of actual errors results in a substantial y
higher probability of the cash rate reaching zero.
D15/259070
2

7
ALTERNATIVE INTEREST RATE PATHS – OCTOBER 2015
Forecast targeting
D15/386771
1

link to page 18 Given the market-implied cash rate path in the baseline scenario, and assuming that
uncertainty around this cash rate forecast is as estimated in
(2015), the probability of a zero cash rate
in early 2018 is about 15 per cent (Graph 2).2
Graph 2
Probability of Zero Cash Rate at Horizon*
%
%
15
15
10
10
5
5
0
0
Jan-16
Jul-16
Jan-17
Jul-17
Horizon
* Based on market-implied cash rate path and the historical ability of zero-
coupon forward rates to forecast the cash rate; assumes forecast errors
are symmetric
Source: RBA
2 This estimate assumes that cash rate forecast errors fol ow the same distribution as the historical distribution of absolute
forecast errors (based on zero-coupon forward rates) and that these errors are symmetrically distributed around the cash rate
forecast; assuming that cash rate forecast errors follow the historical distribution of actual errors results in a substantial y
higher probability of the cash rate reaching zero.
Economist
Economic Research Department
21 October 2015
D15/386771
2

8
ALTERNATIVE INTEREST RATE PATHS – JANUARY 20161
Forecast targeting
D16/25458
1

9
ALTERNATIVE INTEREST RATE PATHS – APRIL 20161
Forecast targeting
D16/135645
1

10
ALTERNATIVE INTEREST RATE PATHS – JULY 20161
Forecast targeting
D16/254859
1

11
ALTERNATIVE INTEREST RATE PATHS – OCTOBER 2016
Forecast targeting
D16/391044
1

12
ALTERNATIVE INTEREST RATE PATHS – JANUARY 2017
Forecast targeting
D17/26813
1

Given the market-implied cash rate path, and
assuming that uncertainty around this cash rate forecast is as estimated in
(2015), the probability of a
zero cash rate at the end of the forecast horizon is 9½ per cent (Graph 2).
Graph 2
Probability of Zero Cash Rate at Horizon*
%
%
10
10
8
8
6
6
4
4
2
2
0
0
Apr-17
Oct-17
Apr-18
Oct-18
Apr-19
Horizon
* Based on market-implied cash rate path and the historical ability
of zero-coupon forward rates to forecast the cash rate; assumes
distribution of forecast errors is symmetric.
Source: RBA
Economic Research Department
25 January 2017
D17/26813
2

13
ALTERNATIVE INTEREST RATE PATHS – APRIL 2017
Forecast targeting
D17/124820
1

Given the market-implied cash rate path, and assuming that uncertainty around this cash rate forecast
is as estimated in
(2015b), the probability of a zero cash rate at the end of the forecast horizon is 9½
per cent (Graph 2).
Graph 2
Probability of Zero Cash Rate at Horizon*
%
%
10
10
8
8
6
6
4
4
2
2
0
0
Jul-17
Jan-18
Jul-18
Jan-19
Jul-19
Horizon
* Based on market-implied cash rate path and the historical ability
of zero-coupon forward rates to forecast the cash rate; assumes
distribution of forecast errors is symmetric.
Source: RBA
Economic Research Department
19 April 2017
D17/124820
2

14
ALTERNATIVE INTEREST RATE PATHS – JULY 2017
Forecast targeting
D17/248278
1

Given the market-implied cash rate path, and assuming that uncertainty
around this cash rate forecast is as estimated in
(2015b), the probability of a zero cash rate at the end of
the forecast horizon is 11 per cent (Graph 2).
Graph 2
Probability of Zero Cash Rate at Horizon*
%
%
10
10
8
8
6
6
4
4
2
2
0
0
Oct-17
Apr-18
Oct-18
Apr-19
Oct-19
Horizon
* Based on market-implied cash rate path and the historical ability
of zero-coupon forward rates to forecast the cash rate; assumes
distribution of forecast errors is symmetric.
Source: RBA
Economic Research Department
19 July 2017
D17/248278
2

Document Outline